I. Introduction▲
L'objectif est d'expliquer, en se basant sur la notion de suite mathématique, comment générer dans une base de données, une suite de valeurs suivant une relation de récurrence. Dans la pratique, on peut par exemple simuler l'évolution des ventes futures en fonction de certains paramètres, et ainsi évaluer le nombre de mois nécessaires pour atteindre un certain seuil.
Pour cela, après avoir présenté la notion de suite mathématique, puis les différents objets de la base Access, on donnera quatre exemples de mise en application :
- progression arithmétique des ventes ;
- progression géométrique des ventes ;
- évolution du capital restant dû ;
- progression des ventes cumulées.
J'ai choisi Access plutôt qu'Excel pour réaliser l'exemple, car le paramétrage et la génération des valeurs de la suite m'ont semblé plus simples depuis un formulaire. D'autre part, la liaison d'un graphique à une source de données dynamique m'a aussi paru plus simple à mettre en œuvre dans Access.
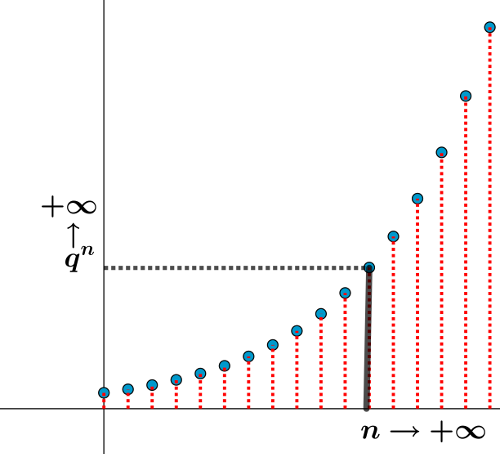
II. Notion de suite mathématique▲
En mathématiques, une suite est une famille d'éléments, appelés ses « termes », indexée par les entiers naturels. Ainsi, les images de 0,1,2,3,...,n sont notées U0,U1,U2,U3,...,Un.
Par la suite on notera U(n) l'image de n par U.
II-A. Suite arithmétique▲
En mathématiques, une suite arithmétique est une suite (le plus souvent une suite numérique) dans laquelle chaque terme permet de déduire le suivant en lui ajoutant une constante appelée raison.
Prenons par exemple la liste des termes :
U(0) = 1
U(1) = 3
U(2) = 5
U(3) = 7
U(4) = 9
...On ajoute donc 2 à chaque terme pour obtenir le suivant. La relation de récurrence de la suite peut alors s'écrire :
U(n+1) = U(n) + 2Et le terme général de cette suite est alors donné par la formule :
U(n) = U(0) + 2*nIl s'agit en fait d'une suite arithmétique de raison 2 et de premier terme 1.
II-B. Suite géométrique▲
En mathématiques, une suite géométrique est une suite de nombres dans laquelle chaque terme permet de déduire le suivant en multipliant par un facteur constant appelé raison.
Prenons maintenant la liste ordonnée des termes :
U(0) = 5
U(1) = 10
U(2) = 20
U(3) = 40
U(4) = 80
...On multiplie bien chaque terme par 2 pour obtenir le suivant. La relation de récurrence de la suite peut alors s'écrire :
U(n+1) = 2*U(n)Et le terme général de cette suite est alors donné par la formule :
U(n) = U(0)*2^nIl s'agit en fait d'une suite géométrique de raison 2 et de premier terme 5.
II-C. Suite arithmético-géométrique▲
En mathématiques, une suite arithmético-géométrique est une suite satisfaisant une relation de récurrence affine, généralisant ainsi les définitions des suites arithmétiques et géométriques.
Prenons la liste ordonnée des termes :
U(0) = 1
U(1) = 3
U(2) = 7
U(3) = 15
U(4) = 31
...La relation de récurrence de la suite peut alors s'écrire :
U(n+1) = 2*U(n) + 1Il s'agit en fait d'une suite arithmético-géométrique de terme initial U0=1 et satisfaisant la relation de récurrence Un+1 = aUn + b, avec a=2 et b=1.
II-D. Suite de sommes partielles▲
Quand on additionne tous les termes d'une suite jusqu’à un certain rang, le résultat de cette opération est ce qu'on appelle une somme partielle.
La suite (Sn) des sommes partielles des termes de (Un) nous donne donc, avec notre notation :
S(0) = U(0)
S(1) = U(0) + U(1)
S(2) = U(0) + U(1) + U(3)
...
S(n) = U(0) + U(1) + ... + U(n)(Un) étant une suite quelconque.
Le terme général de la suite est alors de la forme :
S(n) = U(0) + U(1) + ... + U(n)On peut aussi identifier une relation de récurrence pour cette suite :
S(n+1) = S(n) + U(n+1)Il s'agit donc d'une suite de sommes partielles, notée (Sn), de premier terme S0=U0 et satisfaisant la relation de récurrence Sn+1 = Sn + Un+1.
III. Application▲
On souhaite créer un formulaire permettant de saisir les paramètres d'une suite et de générer ses valeurs successives dans un sous-formulaire affiché en mode feuille de données.
Principe de fonctionnement :
- saisie sur le formulaire des paramètres de la suite ;
- évaluation du nombre de termes de la suite en fonction de ses paramètres ;
- génération des indices et des valeurs des termes de la suite.
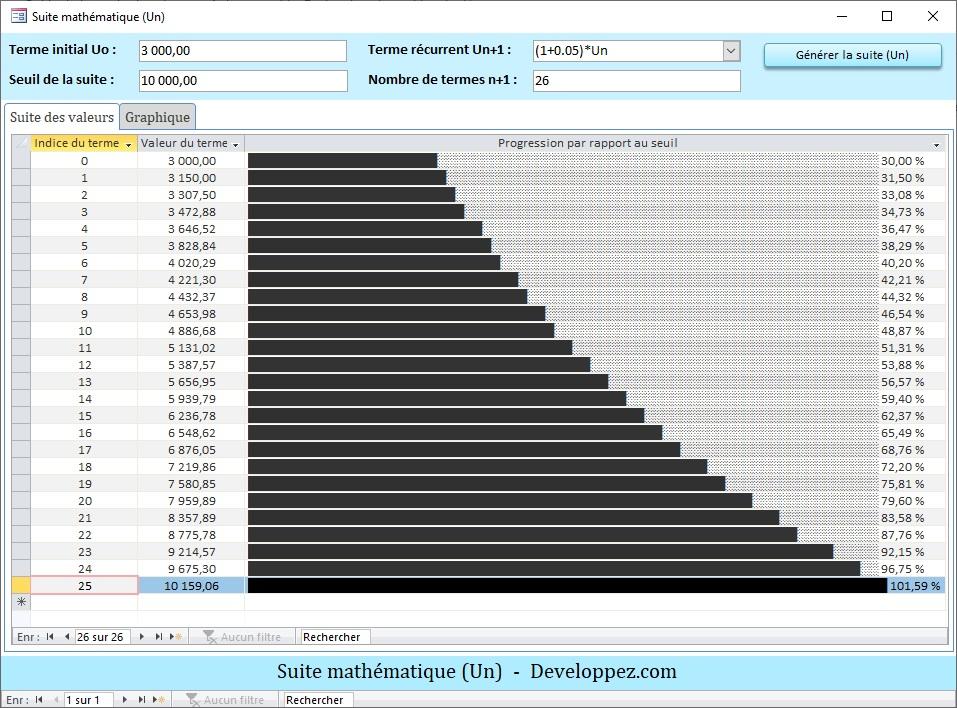
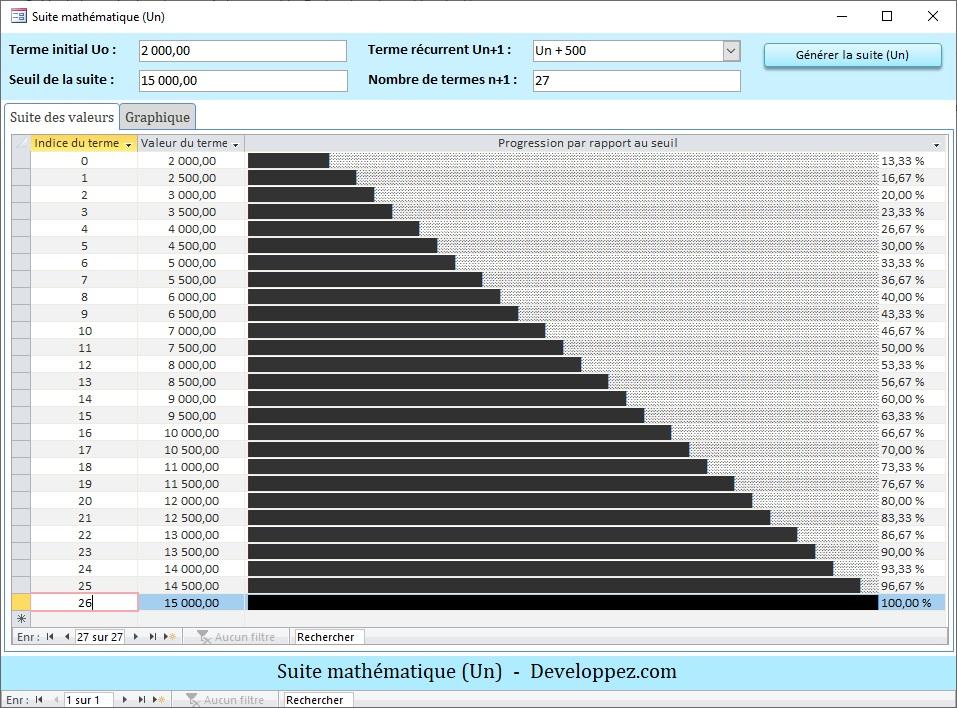
Voici un aperçu du résultat attendu pour une suite géométrique :
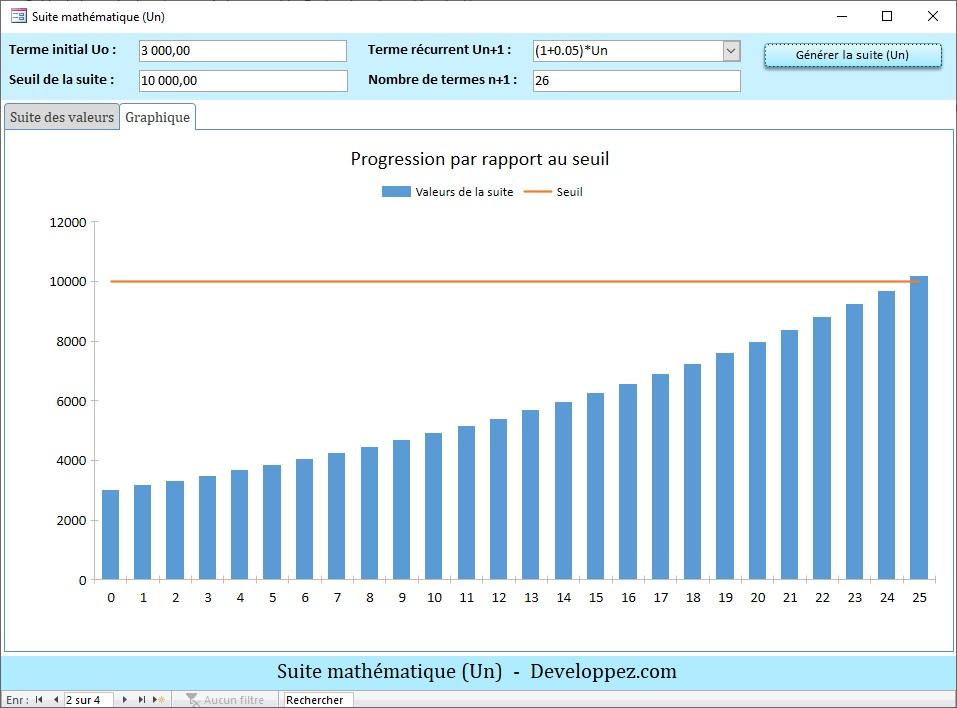
Voici un aperçu du graphique montrant la progression des valeurs de la suite par rapport au seuil :
Nous présentons ensuite les différents objets de la base exemple pour mieux visualiser sa structure.
III-A. Objets de la base exemple▲
III-A-1. Table T_Suite▲
Cette table permet d'enregistrer les paramètres de la suite, comme la valeur du terme initial ou le seuil des valeurs.
|
Nom de la colonne |
Type de données |
Description |
|---|---|---|
|
IdSuite |
Entier long |
Identifiant de la suite |
|
TermeInitial |
Numérique |
Valeur du terme initial de la suite |
|
FormuleRecurrence |
Texte |
Formule de récurrence de la suite |
|
Seuil |
Numérique |
Valeur du seuil de la suite |
|
NombreTermes |
Numérique |
Nombre de termes de la suite |
III-A-2. Table T_ValeursSuite▲
Cette table temporaire permet d'enregistrer les indices et les valeurs de la suite en fonction des paramètres choisis sur le formulaire.
|
Nom de la colonne |
Type de données |
Description |
|---|---|---|
|
IndiceTerme |
Entier long |
Indice du terme de la suite |
|
ValeurTerme |
Numérique |
Valeur du terme de la suite |
|
IdSuite |
Entier long |
Identifiant de la suite pour faire le lien avec la table T_Suite |
La colonne IdSuite permet de faire le lien avec la table T_Suite pour récupérer les paramètres de la suite.
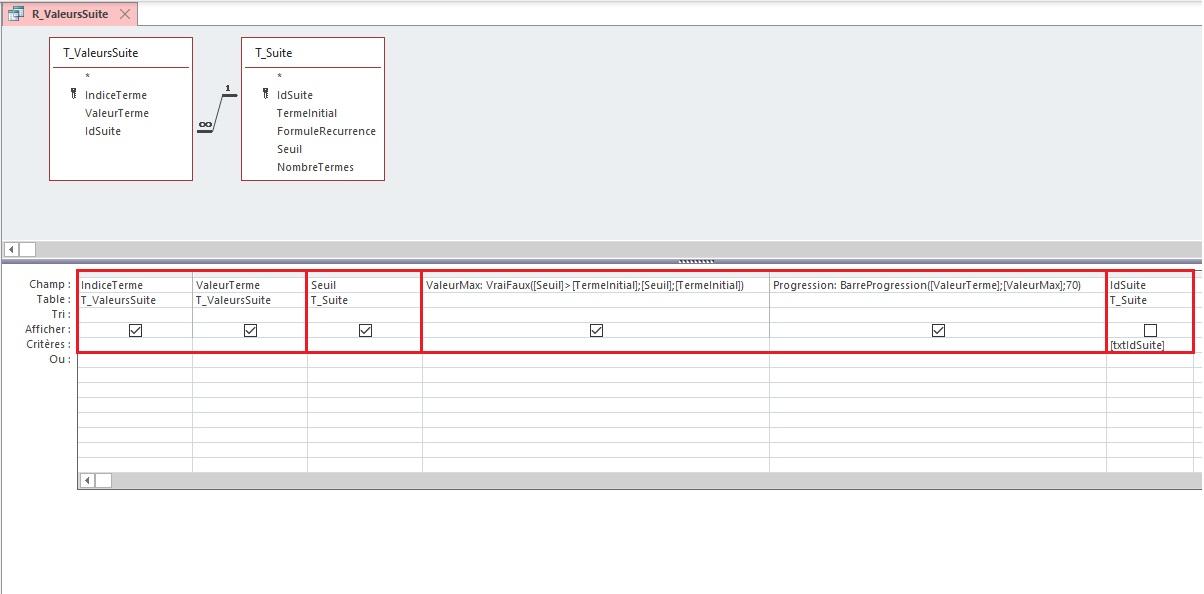
III-A-3. Requête R_ValeursSuite▲
Elle relie les tables T_Suite et T_ValeursSuite sur les colonnes IdSuite et permet d'afficher la liste des valeurs de la suite, avec leur indice et leur progression par rapport au seuil, le tout filtré sur l'identifiant de la suite du formulaire actif.
La formule pour afficher la progression de la suite (Un) par rapport au seuil :
Progression: BarreProgression([ValeurTerme];[ValeurMax];70)On utilise dans cette formule la fonction BarreProgression qui renvoie une chaîne de caractères sous la forme d'une barre de progression.
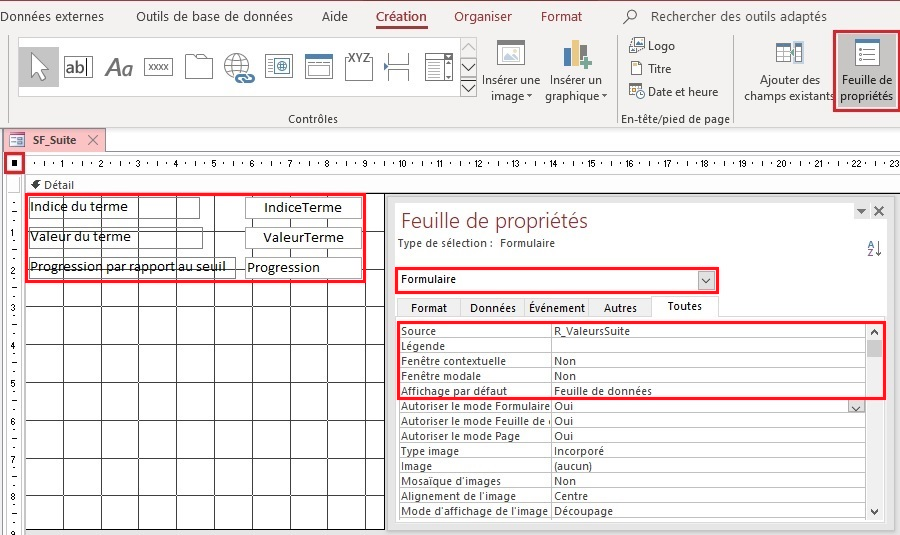
III-A-4. Sous-formulaire SF_ValeursSuite▲
Il est lié à la requête R_ValeursSuite et contient les zones de texte reliées aux colonnes IndiceTerme, ValeurTerme et Progression.
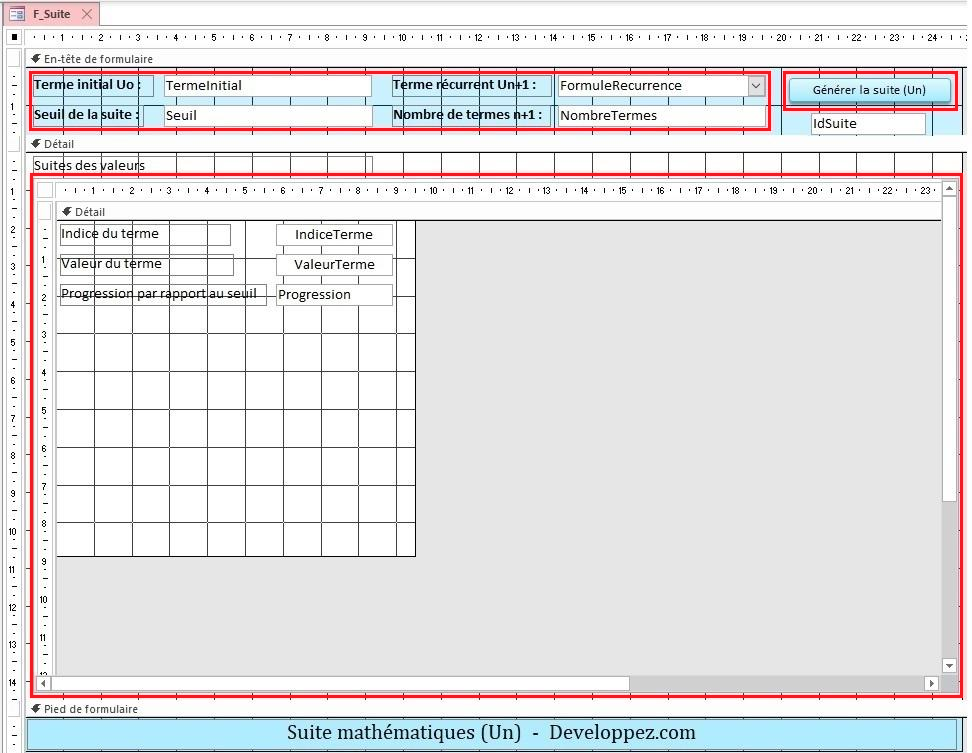
III-A-5. Formulaire F_Suite▲
Il permet de saisir les paramètres de la suite et de générer ses termes dans le sous-formulaire.
Il comprend, en plus du sous-formulaire, les contrôles suivant :
- une zone de texte txtTermeInitiale pour saisir le terme initial de la suite ;
- une liste déroulante cmbFormuleRecurrence pour saisir la formule de récurrence avec le terme Un ;
- une zone de texte txtSeuil pour indiquer le seuil à atteindre ;
- une zone de texte txtNombreTermes pour indiquer le nombre de termes de la suite ;
- un bouton de commande cmdGenererSuite pour générer la suite ;
- un contrôle graphique grpSuite pour représenter la progression de la suite par rapport au seuil.
III-A-5-a. Bouton de commande cmdGenererValeursSuite▲
Il permet de générer la suite des termes en fonction des paramètres saisis sur le formulaire.
Déroulé de la procédure :
- on teste si tous les paramètres de la suite ont été saisis ;
- si c'est le cas, on génère la suite de termes ;
- on rafraîchit le sous-formulaire SF_ValeursSuite et le graphique grpSuite.
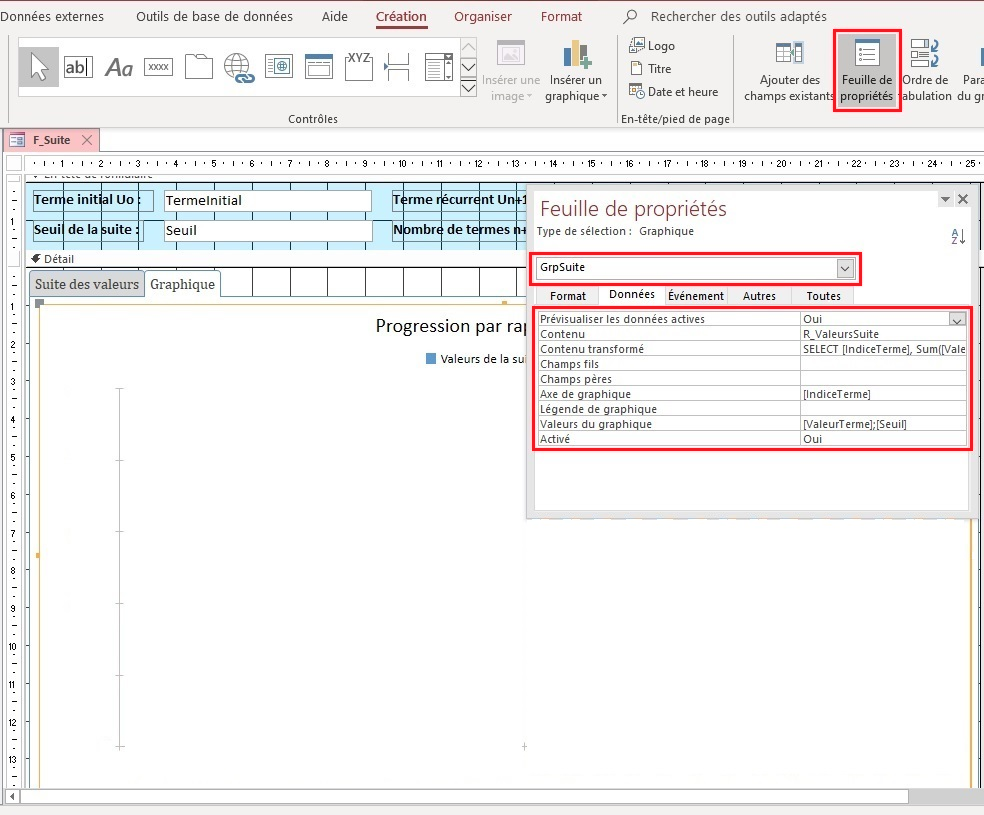
III-A-5-b. Contrôle graphique grpSuite▲
Il permet de représenter sous la forme d'un histogramme la progression de la suite par rapport au seuil choisi.
Le graphique a comme source de données la requête R_ValeursSuite. Il comprend, en abscisse, les indices de la suite et en ordonnée, les valeurs de la suite et du seuil limite.
III-A-6. Module M_GenererValeursSuite▲
III-A-6-a. Procédure GenererValeursSuite▲
Déroulé de la procédure :
- on vide la table T_ValeursSuite ;
- puis, on évalue chaque terme de la suite ;
- pour chaque terme, on ajoute sa valeur et son indice dans la table T_ValeursSuite.
On utilise la fonction Eval pour évaluer les expressions obtenues à partir des relations de récurrence.
III-A-6-b. Fonction EvalNombreTermes▲
Permet d'évaluer le nombre de termes de la suite en fonction du terme initial, de la formule de récurrence et du seuil saisis sur le formulaire.
Déroulé de la procédure :
- on évalue chaque terme de la suite ;
- pour chaque terme, on teste si sa valeur est supérieure ou égale au seuil ;
- si ce n'est pas le cas, on passe au terme suivant ;
- si c'est le cas, on sort en renvoyant l'indice du dernier terme.
Public Function evalNombreTermes(ByVal Uo As Double, ByVal FormuleRecurrence As String, ByVal Seuil As Double) As Long
' Détermine le nombre de termes de la suite
' U0 : ' argument pour la valeur du terme initial
' FormuleRecurrence : ' argument pour la formule du terme d'indice n
' Seuil : ' argument contenant la valeur du seuil
Dim i As Long, n As Long, Un As Double, s As Integer
Un = Uo ' on initialise le terme de la série
i = 1 ' on initialise l'indice des termes de la série
s = Sgn(Seuil - Un) ' signe de la différence entre le seuil et Un
Do While Sgn(Seuil - Un) = s ' tant qu'on n’a pas atteint le seuil
s = Sgn(Seuil - Un) ' signe de la différence entre le seuil et Un
Un = EvalExpression(FormuleRecurrence, Un, i) ' évaluation de la formule de récurrence pour n=i
i = i + 1 ' on incrémente l'indice des termes de la série
If i > 2000 Then Exit Do ' on définit une limite pour sortir avant que le seuil soit atteint
Loop
evalNombreTermes = i ' on renvoie l'indice du dernier terme dont la valeur est supérieure ou égale au seuil
End FunctionLa fonction est déclarée publique pour pouvoir l'appeler dans tout le projet.
III-A-6-c. Fonction EvalExpression▲
Permet d'évaluer l'expression obtenue à partir de la formule de récurrence.
On a recours pour cela à la fonction Eval disponible dans l'environnement VBA Access.
Syntaxe
Eval(expression)
L'argument expression est une expression qui prend la valeur d’une chaîne de texte alphanumérique. Par exemple, l’argument expression chaîne peut être une fonction qui retourne une chaîne ou une valeur numérique.
Exemples d'utilisation :
Debug.Print Eval("2+3")
renvoie 5
Debug.Print Eval("2*3")
renvoie 6
...Déroulé de la fonction :
- on identifie le terme Un dans la formule avec sa valeur ;
- on identifie l'indice n dans la formule avec sa valeur ;
- on évalue l'expression obtenue avec la fonction Eval.
Private Function EvalExpression(ByVal FormuleRecurrence As String, ByVal Un As Double, ByVal n As Long) As Double
' Evalue l'expression obtenue à partir de la formule de récurrence
' FormuleRecurrence : ' argument pour la formule du terme d'indice n
' Un : ' argument pour la valeur du terme d'indice n
' n : ' argument contenant l'indice n de la suite
' la formule est du type : n*Un + 10, il faut identifier Un dans cette formule
FormuleRecurrence = Replace(FormuleRecurrence, "Un", Replace(CStr(Un), ",", "."))
FormuleRecurrence = Replace(FormuleRecurrence, "n", CStr(n)) ' puis, on identifie n dans la formule
EvalExpression = Eval(FormuleRecurrence) ' enfin, on évalue l'expression obtenue
End FunctionIII-A-6-d. Fonction BarreProgression▲
Elle renvoie une chaîne de caractères sous la forme d'une barre de progression.
Public Function BarreProgression(valeur As Double, valeurMax As Double, maximum As Long) As String
' valeur : argument indiquant la valeur de la suite pour un certain indice
' valeurMax : argument indiquant la valeur maxi de la suite
' maximul : argument indiquant la valeur maxi de la barre de progression
Dim pp As Double, pg As Long, pr As Long
pp = valeur / valeurMax ' proportion par rapport au total
pg = CInt(pp * maximum) ' progression par rapport à la valeur maxi de la barre
pr = (maximum - pg) ' progression restante
If pg < 0 Then ' si la progression pg est négative
pg = 0 ' on met 0 pour la progression
pr = maximum
End If
If pr < 0 Then ' si la progression pg est supérieure à la valeur maxi
pr = 0 ' on a 0 pour le reste de la progression
End If
' On renvoie la progression de la suite sous la forme d'une barre de progression composée d'une chaîne de caractères
BarreProgression = String(pg, ChrW(&H2588)) & String(pr, ChrW(&H2591)) & " " & Format(pp, "0.00 %")
End FunctionIII-B. Progression linéaire des ventes▲
On a constaté que les ventes d'un certain produit augmentent approximativement de p euros par mois.
En partant d'un montant initial des ventes, noté U0=m, on souhaite donc estimer suivant ce modèle les montants des ventes pour chacun des n mois suivants.
Le montant attendu le mois suivant sera donc :
U(1) = m + pEn généralisant, on obtient donc la suite des montants mensuels :
U(0) = m
U(1) = m + p
U(2) = (m + p) + p = m + 2*p
U(3) = ((m + p) + p) + p = m + 3*p
...
U(n) = (...((m + p) + p) + p) + ...) + p = m + n*pOn a bien une suite arithmétique de raison p et de terme initial U0=m.
La relation de récurrence de la suite est donnée par :
U(n+1) = U(n) + pLe terme général de cette suite est donc :
U(n) = m + n*pavec Un le terme d'indice n de la suite (Un).
Si on prend U0=2000 et p=500, on obtient avec la fonction Eval, la suite des valeurs :
U(0) = 2000
U(1) = Eval("2000 + 500") = 2500
U(2) = Eval("2500 + 500") = 3000
U(3) = Eval("3000 + 500") = 3500
...
U(n+1) = Eval("U(n) + p") = ...Aperçu de la suite arithmétique obtenue :
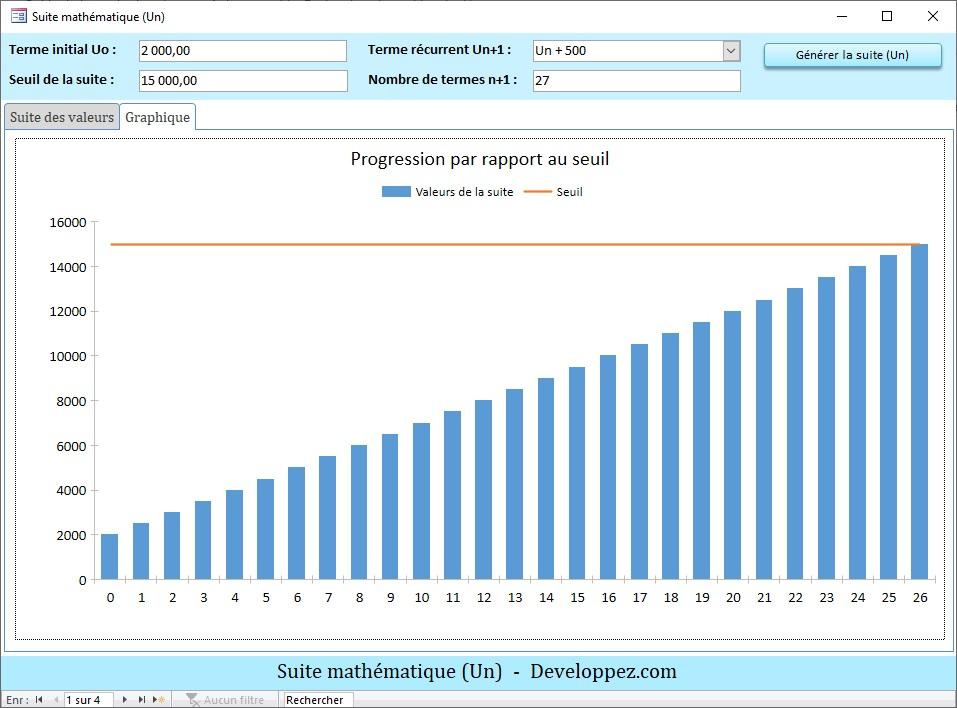
Aperçu du graphique correspondant :
La formule de récurrence employée pour la progression arithmétique est notée Un+1 = Un + 500.
On peut également utiliser le terme général noté Un+1 = 2000 + 500*(n+1).
III-C. Progression géométrique des ventes▲
On a constaté que les ventes d'un certain produit progressent en suivant un taux d'évolution mensuel proche de t.
En partant toujours d'un montant initial des ventes, noté U0=m, on souhaite donc prévoir suivant ce modèle les montants des ventes pour chacun des n mois suivants.
Le montant attendu le mois suivant sera donc :
U(1) = m + m*t
U(1) = m*(1+t)En généralisant, on obtient ainsi la suite des montants mensuels :
U(0) = m
U(1) = m*(1+t)
U(2) = m*(1+t)*(1+t) = m*(1+t)^2
U(3) = m*(1+t)*(1+t)*(1+t) = m*(1+t)^3
...
U(n) = m*(1+t)^nOn a bien une suite géométrique de raison (1+t) et de terme initial U0=m.
La relation de récurrence est donnée cette fois par :
U(n+1) = (1+t)*U(n)Cette égalité conduit logiquement à la formule du taux d'évolution :
t = (U(n+1) - U(n))/U(n)Le terme général de cette suite est alors :
U(n) = m*(1+t)^navec Un le terme d'indice n de la suite (Un).
Si on prend U0=3000 et t=0.05, on obtient avec la fonction Eval, la suite des valeurs :
U(0) = 3000
U(1) = Eval("(1 + 0.05)*3000") = 3150
U(2) = Eval("(1 + 0.05)*3150") = 3307.5
...
U(n+1) = Eval("(1 + 0.05)*U(n)") = ...Aperçu de la suite géométrique obtenue :
Aperçu du graphique correspondant :
La relation de récurrence employée pour la progression géométrique est notée ici Un+1 = (1 + 0.05)*Un.
On constate aussi que le seuil de 10 000 est atteint et dépassé à partir du 25e mois.
III-D. Évolution du capital restant dû▲
Un capital c emprunté à un taux mensuel t et remboursé par mensualités constantes m conduit à la construction d'une suite arithmético-géométrique. Si Rn représente le capital restant dû au bout de n mensualités, la suite (Rn), est définie par la relation de récurrence :
Rn+1 = (1+t)*Rn - mPour un capital de départ c=10000, un taux mensuel t=0.004 et un remboursement mensuel de m=400, on aboutit donc à la formule de récurrence :
Rn+1 = (1 + 0.004)*Rn - 400
Un+1 = (1 + 0.004)*Un - 400Ce qui peut également s'écrire :
U(n+1) = (1 + 0.004)*U(n) - 400Avec le terme initial :
U(0) = 10000On obtient, avec la fonction Eval, la suite des valeurs :
U(0) = 10000
U(1) = Eval("(1 + 0.004)*10000 - 400") = 9640
U(2) = Eval("(1 + 0.004)*9640 - 400") = 9278.56
...
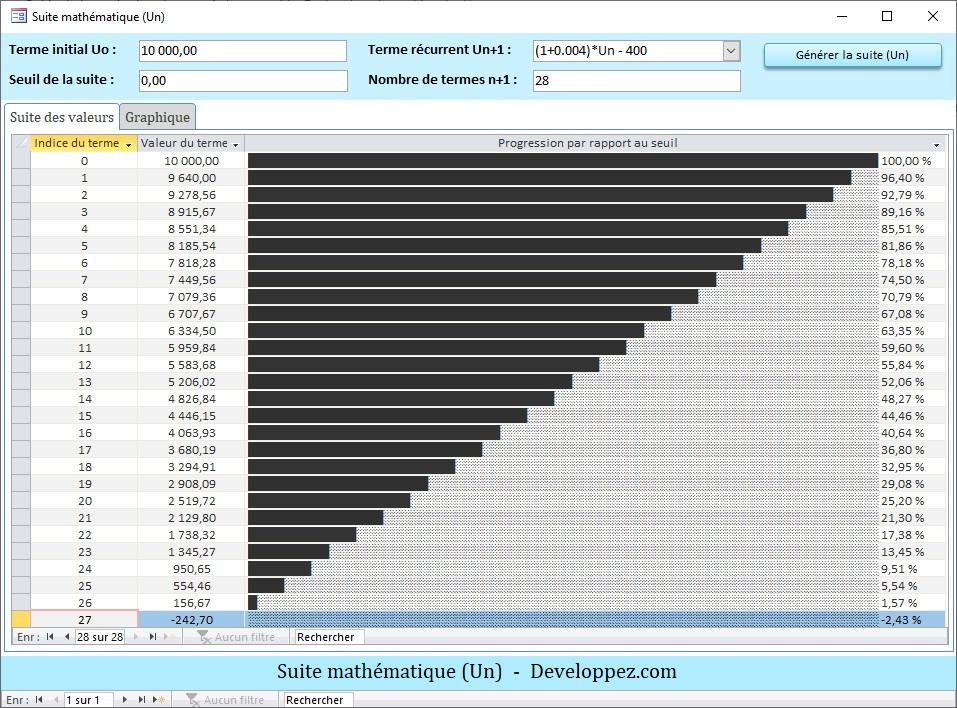
U(n+1) = Eval("(1 + 0.004)*U(n) - 400") = ...Aperçu de l'évolution du capital restant à rembourser :
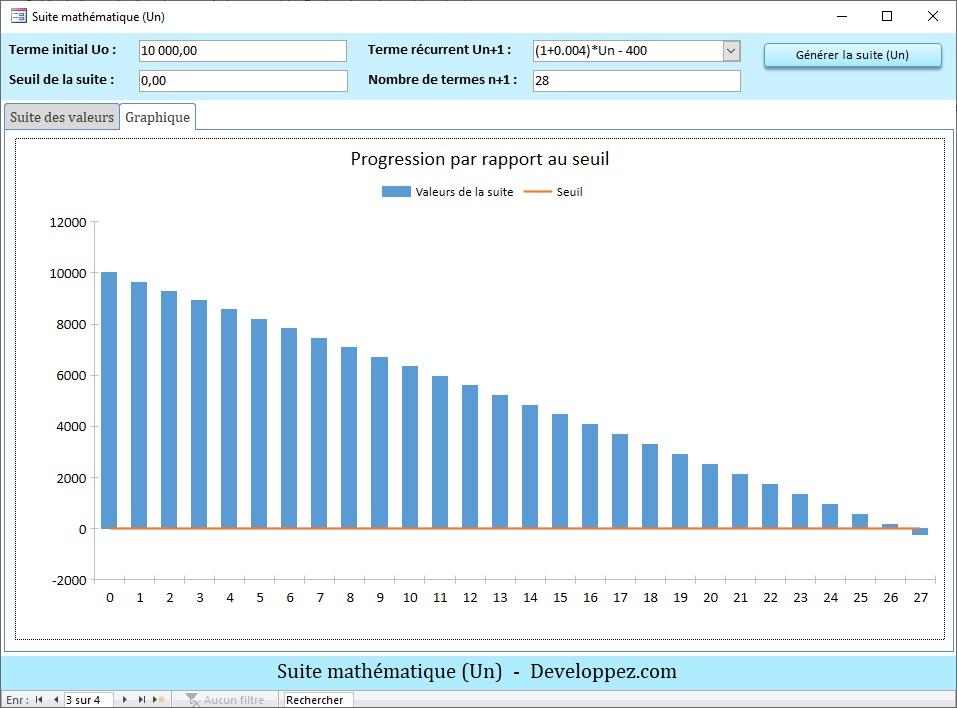
Aperçu du graphique correspondant :
La relation de récurrence employée pour la progression arithmético-géométrique est notée ici Un+1 = (1 + 0.004)*Un - 400.
On constate aussi que le capital restant dû devient inférieur à 0, à partir du 27e mois.
III-E. Progression des ventes cumulées▲
En partant toujours d'un montant initial des ventes, noté U0=m, on souhaite obtenir les valeurs cumulées des ventes pour chacun des n mois suivants, en appliquant pour chaque mois un taux d'évolution t.
Le montant cumulé du mois suivant est alors :
S(1) = U(0) + (U(0) + t*U(0))
S(1) = U(0) + U(0)*(1+t)On obtient ainsi la suite des n montants cumulés suivant la valeur initiale :
S(0) = U(0) = m
S(1) = U(0) + U(1) = m + m*(1+t)
S(2) = U(0) + U(1) + U(2) = m + m*(1+t) + m*(1+t)*(1+t) = m + m*(1+t) + m*(1+t)^2
S(3) = U(0) + U(1) + U(2) + U(3) = m + m*(1+t) + m*(1+t)^2 + m*(1+t)^3
...
S(n) = U(0) + ... + U(n) = m + m*(1+t) + ... + m*(1+t)^nOn a bien une suite de sommes partielles des termes d'une progression géométrique, notée Sn et de terme initial S0=m.
Le terme général de cette suite est donc :
S(n) = m + m*(1+t) + ... + m*(1+t)^nLa relation de récurrence de la suite est donnée par :
S(n+1) = S(n) + m*(1 + t)^(n+1)avec Sn le terme d'indice n de la suite (Sn).
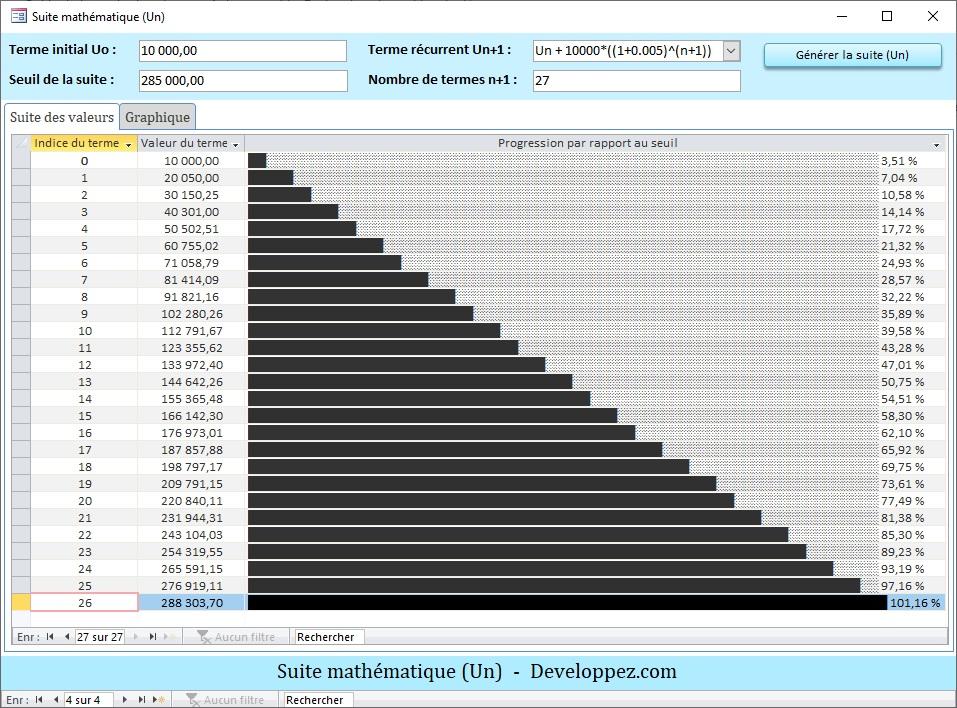
Aperçu de la suite Sn pour m=10000 et t=0.005, soit un taux d'évolution mensuel de 0.5% :
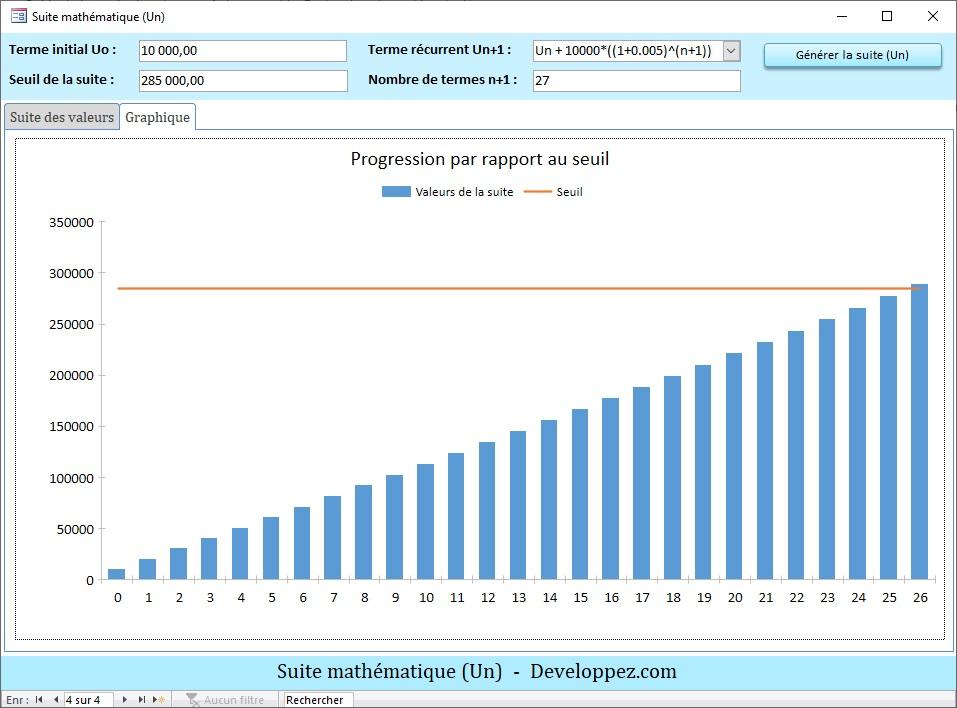
Aperçu du graphique correspondant :
La relation de récurrence employée pour la progression des cumuls est notée ici Un+1 = Un + 10000*((1 + 0.005)^(n+1)).
On constate aussi que le seuil de 285 000 est atteint et dépassé à partir du 26e mois.
IV. Conclusion▲
Dans la pratique, les suites récurrentes peuvent donc permettre, par exemple, de réaliser des simulations pour savoir au bout de combien de mois un certain seuil est atteint ou dépassé. Il suffit pour cela d'identifier leur relation de récurrence et leurs paramètres, pour ensuite pouvoir générer les valeurs successives.
V. Base de données à télécharger▲
La base jointegenerer-suites-recurrentes est au format accdb.
VI. Remerciements▲
Je tiens à remercier jeannot45, Laurent Ott et Pierre Fauconnier pour m'avoir conseillé pour la réalisation de cet article, ainsi que escartefigue pour sa relecture.