I. Introduction▲
Récursivité : en informatique et en logique, une fonction ou plus généralement un algorithme qui contient un appel à lui-même est dit récursif.
Nombreux sont les exemples dans lesquels on utilise la récursivité :
- fonctions mathématiques récursives, comme la factorielle ;
- représentation et évaluation d'expressions arithmétiques composées de plusieurs opérations ;
- génération des arrangements ou des combinaisons de p éléments pris dans n ;
- création d'un arbre généalogique à partir d'informations stockées dans une base de données.
Nous présenterons pour commencer deux exemples simples de fonctions mathématiques récursives écrites en VBA, accompagnées de schémas affichant les structures d'appels récursifs. Enfin, dans la 3e partie, nous étudierons le cas de la génération et de l'évaluation d'expressions arithmétiques à partir de données enregistrées dans une base Access.
II. Exemples de fonctions récursives▲
Commençons par décrire des exemples simples de fonctions mathématiques récursives.
II-A. Fonction factorielle▲
En mathématiques, la factorielle d'un entier naturel n est le produit des nombres entiers strictement positifs inférieurs ou égaux à n.
Si on considère la fonction Fact(n) donnant la factorielle de n, les premières valeurs de cette fonction sont :
Fact(0) = 1
Fact(1) = 1
Fact(2) = (1)*2 = 2
Fact(3) = (1*2)*3 = 6
Fact(4) = ((1*2)*3)*4 = 24
...On voit que la récursivité de la fonction factorielle peut être définie par l'expression :
Fact(n)=Fact(n-1)*navec :
Fact(0)=1Pour n=0, la fonction vaut 1. Comme on le verra plus loin, cette condition permet l'arrêt des appels récursifs de la fonction VBA et la remontée des résultats.
II-A-1. Code VBA▲
Sa traduction en VBA est assez simple :
'*********************************************************************************************************************
'**************************************Fonction récursive de la factorielle*******************************************
'*********************************************************************************************************************
Function Fact(n As Long) As Long
' n: argument de la factorielle
If n = 0 Then ' condition de sortie et d'arrêt des appels récursifs
Fact = 1
Else
' appel de la fonction pour (n-1)
Fact = Fact(n - 1) * n ' remontée du résultat pour Fact(n-1) et calcul de Fact(n)
End If
End FunctionPour ne pas compliquer les choses, on ne traite pas le cas où la valeur entrée est inférieure à 0 (n<0).
II-A-2. Structure des appels et remontée des résultats▲
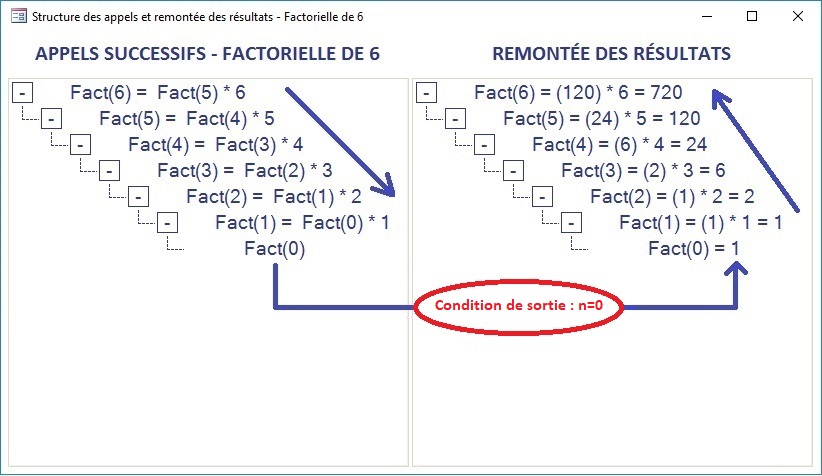
La fonction génère des appels récursifs successifs pour Fact(n), Fact(n-1),..,Fact(0), puis remonte les résultats à partir de Fact(0)=1 (condition de sortie), puis Fact(1)=Fact(0)*1=1*1,.., Fact(n)=Fact(n-1)*n, suivant le schéma :
Pour afficher les différentes structures d'appels des fonctions, on utilise le contrôle CtrlTree inséré dans un formulaire. Il nécessite l'installation d'une bibliothèque. Pour plus de détails, vous pouvez consulter la page Librairie pour arbres, grilles et listes sous AccessLibrairie pour arbres, grilles et listes sous Access.
II-B. Fonction de Fibonacci▲
La suite de Fibonacci est une suite d'entiers dans laquelle chaque terme est la somme des deux termes qui le précèdent. Elle commence généralement par les termes 0 et 1 (parfois 1 et 1) et ses premiers termes sont : 0, 1, 1, 2, 3, 5, 8, 13, 21, etc.
Si on considère la fonction Fibo(n) donnant les termes de cette suite d'indice n, les premières valeurs de cette fonction sont :
Fibo(0) = 0
Fibo(1) = 1
Fibo(2) = 1 + 1 = 2
Fibo(3) = 1 + 2 = 3
Fibo(4) = 2 + 3 = 5
...Sa récurrence peut ainsi être définie par l'expression :
Fibo(n)=Fibo(n-2)+Fibo(n-1)ou encore par son équivalent :
Fibo(n)=Fibo(n-1)+Fibo(n-2)avec :
Fibo(0)=0
Fibo(1)=1Pour n=0 et n=1, la fonction vaut respectivement 0 et 1. Comme on le verra plus loin pour la fonction VBA, ces conditions permettent l'arrêt des appels récursifs et la remontée des résultats.
II-B-1. Code VBA▲
Sa traduction en VBA ne pose pas de problème particulier :
'*********************************************************************************************************************
'***********************************Fonction récursive de la suite de Fibonacci***************************************
'*********************************************************************************************************************
Function Fibo(n As Long) As Long
' n: nombre de termes de la suite de Fibonacci
If (n = 0) Then ' condition de sortie et d'arrêt des appels récursifs
Fibo = 0
ElseIf (n = 1) Then ' condition de sortie et d'arrêt des appels récursifs
Fibo = 1
Else
' appel de la fonction Fibo pour (n-2) et (n-1)
Fibo = Fibo(n - 2) + Fibo(n - 1) ' remontée du résultat pour Fibo(n-2) et Fibo(n-1), puis calcul de Fibo(n)
End If
End FunctionPour ne pas compliquer les choses, on ne traite pas le cas où la valeur entrée est inférieure à 0 (n<0).
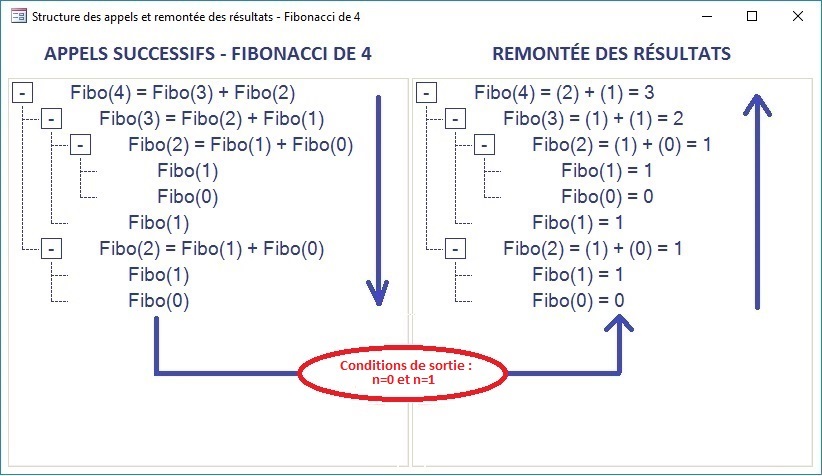
II-B-2. Structure des appels et remontée des résultats▲
La fonction génère des appels récursifs successifs pour Fibo(n), Fibo(n-1),..,Fibo(0), puis remonte les résultats à partir de Fibo(0)=0 et Fibo(1)=1 (conditions de sortie), puis Fibo(2)=Fibo(0)+Fibo(1) = 1 + 1,.., Fibo(n)=Fibo(n-2)+Fibo(n-1), suivant le schéma :
II-C. Limites de la récursivité▲
Même si les fonctions récursives peuvent être un moyen commode et élégant pour résoudre des problèmes variés, elles ont aussi leur limite au niveau du stockage des données en mémoire, et peuvent ainsi provoquer assez rapidement des débordements de pile (stack Overflow).
Illustrons ce cas de figure avec la fonction Sigma(n) qui calcule la somme des n premiers entiers en partant de 1 :
'*********************************************************************************************************************
'*************************************Fonction Sigma - somme des n premiers entiers***********************************
'*********************************************************************************************************************
Function Sigma(ByVal n As Long) As Long
' n: nombre d'entiers sommés
If n = 1 Then ' condition de sortie et d'arrêt des appels récursifs
Sigma = 1 ' renvoie 1
Else
' appel de la fonction pour (n-1)
Sigma = Sigma(n - 1) + n ' remontée du résultat pour Sigma(n-1) et calcul de Sigma(n)
End If
End FunctionPour éviter l'erreur de dépassement de capacité rencontrée pour de grandes valeurs, il vaut mieux préférer le type Long (entier long) au type Integer (entier court).
II-C-1. Empilement et remontée▲
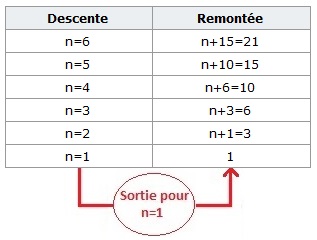
La phase de descente et de remontée dans la pile des appels de la fonction récursive pour Sigma(6) :
Au cours de la phase de descente, les valeurs des arguments de n=6 à n=1 sont donc stockées successivement dans la pile et ce n'est qu'au moment de la remontée, donc également au moment où la condition de sortie est vraie, que les appels enregistrés sont dépilés au fur et à mesure de la remontée. Ici pour des petits calculs cela convient très bien, mais lorsqu'il s'agit de faire de plus profondes récursions cela peut provoquer un dépassement de capacité avec un espace de pile insuffisant.
Pour plus de détails, je vous invite à consulter la page Récursivité en langage CRécursivité en langage C.
II-C-2. Débordement de pile (stack overflow)▲
La pile est un emplacement mémoire destiné à mémoriser les paramètres, les valeurs des variables locales, mais aussi les adresses des fonctions en cours d'exécution. Le volume de données est donc important et un débordement de la pile peut très vite arriver.
Pour le vérifier, déterminons à partir de quel entier Sigma génère un débordement de pile.
Pour cela, on va écrire une fonction principale comportant une gestion d'erreur, qui va appeler dans une boucle la fonction Sigma successivement pour 1, 2, 3… jusqu'à provoquer l'erreur de dépassement de pile pour un entier n<10000, erreur que l'on récupérera dans la routine principale pour afficher la valeur de n.
'********************************************************************************************************************
'***************************************Fonction test du débordement de pile*****************************************
'********************************************************************************************************************
Public Function TesterSigma() As Long
On Error GoTo err_TesterSigma ' gestion d'erreur
Dim i As Long
For i = 1 To 100000
Call Sigma(i) ' appel de la fonction pour i
Next i
Exit Function
err_TesterSigma:
Debug.Print Err.Description + " pour Sigma(" + i + ")" ' affichage de l 'erreur
End FunctionAvec ma machine, j'obtiens un débordement de pile pour n proche de 6284, cette valeur pouvant varier en fonction de la mémoire de la pile d'appels. En VBA, la mémoire de la pile d'appels étant très petite, on est très vite bloqué.
II-D. Fonctions récursives terminales▲
On peut aussi réécrire les fonctions récursives pour éviter la remontée des résultats et donc leur empilement.
Function récursionNonTerminale(n)
...
récursionNonTerminale = n + récursionNonTerminale(n - 1)
End FunctionDans ce cas, on remarque que l'instruction est une expression faisant intervenir l'appel récursif, tous les résultats intermédiaires doivent donc être conservés en mémoire.
Function récursionTerminale(n)
...
récursionTerminale = récursionTerminale(n - 1)
End FunctionIci, aucune référence aux résultats précédents n'est à conserver en mémoire.
Si on reprend l'exemple de la somme des n premiers entiers, suivant ce principe la fonction récursive terminale Sigma2 nécessite alors un 2e argument s, nommé accumulateur, pour calculer la somme :
'*********************************************************************************************************************
'******************************************Fonction récursive terminale Sigma2****************************************
'*********************************************************************************************************************
Function Sigma2(ByVal n As Long, ByVal s As Long) As Long
' n: nombre d'entiers sommés
If n = 1 Then ' condition de sortie et d'arrêt des appels récursifs
Sigma2 = s ' renvoie la somme s terminale, sans remontée de résultat
Else
' appel de la fonction pour (n-1)
Sigma2 = Sigma2(n - 1, s + (n - 1)) ' calcul de la somme dans le 2e argument
End If
End FunctionSchéma des appels récursifs de la fonction pour Sigma2(6,6) :
Le schéma montre qu'il n'y a qu'une phase de descente, mais pas de remontée. De cette manière nous économisons l'utilisation de la pile du programme, et nous gagnons également du temps en exécution.
III. Récursivité et opérations arithmétiques▲
Une expression arithmétique peut être représentée par une structure arborescente :
Pour créer une expression arithmétique, on a besoin d'enregistrer dans une table T_Operation, les différentes opérations et leurs liens.
III-A. Table nécessaire▲
III-A-1. T_Operation▲
|
Nom du champ |
Type du champ |
Description |
|---|---|---|
|
NumOperation |
Entier long |
Numéro de l'opération |
|
Valeur1 |
Numérique |
Opérande n°1 à gauche de l'opérateur |
|
Operateur |
Texte |
Opérateur arithmétique : +, -, *, / |
|
Valeur2 |
Numérique |
Opérande n°2 à droite de l'opérateur |
|
IDOperationDescendante1 |
Entier long |
Clé étrangère qui identifie la sous-opération correspondant au terme de gauche |
|
IDOperationDescendante2 |
Entier long |
Clé étrangère qui identifie la sous-opération correspondant au terme de droite |
III-B. Requêtes▲
III-B-1. R_Operations (1)▲
Requête servant de base pour le calcul des résultats intermédiaires :
SELECT NumOperation, Valeur1, Operateur, Valeur2, Switch([Operateur]="+",[Valeur1]+[Valeur2],[Operateur]="-",[Valeur1]-[Valeur2],[Operateur]="*",[Valeur1]*[Valeur2],[Operateur]="/",[Valeur1]/[Valeur2]) AS Resultat, IdOperationDescendante1, IdOperationDescendante2
FROM T_Operation
ORDER BY NumOperation;Dans laquelle le champ calculé :
Resultat : Switch([Operateur]="+",[Valeur1]+[Valeur2],[Operateur]="-",[Valeur1]-[Valeur2],[Operateur]="*",[Valeur1]*[Valeur2],[Operateur]="/",[Valeur1]/[Valeur2])Permet de calculer le résultat de chaque opération arithmétique.
III-B-2. R_Operations (2)▲
Requête servant de base à la fonction VBA pour le calcul de l'expression arithmétique :
SELECT NumOperation, Valeur1, Operateur, Valeur2, Switch([Operateur]="+",[Valeur1]+[Valeur2],[Operateur]="-",[Valeur1]-[Valeur2],[Operateur]="*",[Valeur1]*[Valeur2],[Operateur]="/",[Valeur1]/[Valeur2]) AS Resultat, IdOperationDescendante1, IdOperationDescendante2, (Select Max(NumOperation) as m from T_Operation As T1 where (Not IsNull(IdOperationDescendante1)) or( Not IsNull(IdOperationDescendante2)))=[NumOperation] AS Racine
FROM T_Operation
ORDER BY NumOperation;Dans laquelle la sous-requête :
(Select Max(NumOperation) as m from T_Operation As T1 where (Not IsNull(IdOperationDescendante1)) or( Not IsNull(IdOperationDescendante2)))Permet de savoir si l'opération est à la racine dans la structure arborescente de l'expression arithmétique.
III-C. Affichage des données▲
Liste des opérations composant l'expression arithmétique
|
NumOperation |
Valeur1 |
Operateur |
Valeur2 |
Resultat |
IDOperationDescendante1 |
IDOperationDescendante2 |
|---|---|---|---|---|---|---|
|
1 |
10 |
+ |
20 |
30 |
||
|
2 |
2 |
* |
5 |
10 |
||
|
3 |
30 |
* |
10 |
300 |
1 |
2 |
|
4 |
300 |
+ |
50 |
350 |
3 |
|
|
5 |
350 |
* |
10 |
3500 |
4 |
|
|
6 |
3500 |
/ |
100 |
35 |
5 |
Les valeurs en rouge sont calculées. Le formulaire F_Operations présent dans la base jointe permet une saisie simplifiée des différentes opérations.
III-D. Fonction VBA▲
La fonction EvalExpression explore de façon récursive, les différentes opérations contenues dans la requête en partant de la racine :
'*********************************************************************************************************************
'***************************Fonction appelante pour évaluer l'expression arithmétique ********************************
'*********************************************************************************************************************
Public Function EvaluerExpression()
Dim db As DAO.Database
Dim rs As DAO.Recordset
Set db = CurrentDb
Set rs = db.OpenRecordset("R_Operations (2)", dbOpenDynaset) ' ouverture de la requête dans le recordset
rs.FindFirst ("Racine=true") ' Position à la racine, opération sans ascendant
EvaluerExpression = EvalExpression(rs, rs.Bookmark) ' appel de la fonction récursive
' Libération des variables
rs.Close
Set rs = Nothing
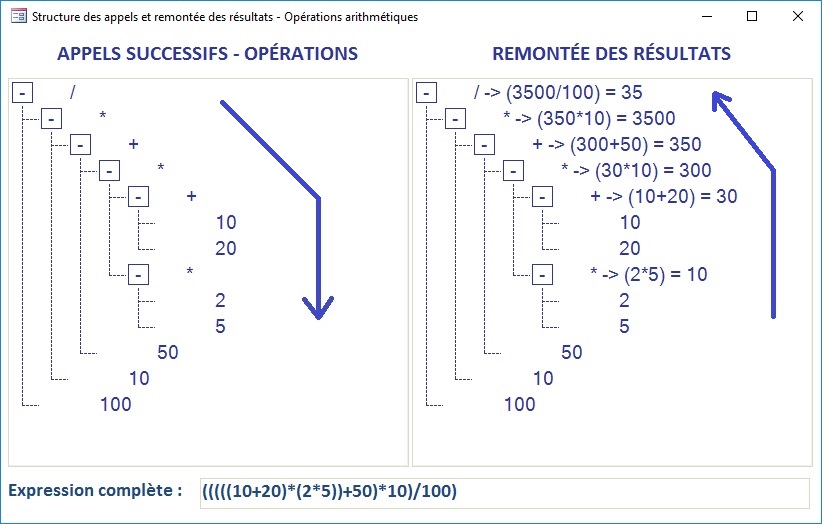
End FunctionIII-E. Structure des appels et remontée des résultats▲
La fonction génère des appels récursifs successifs pour l'expression (((((10+20)*(2*5))+50)*10)/100), suivant le schéma :
IV. La base de données à télécharger▲
La base jointeBD Récursivité présente les exemples décrits dans le tutoriel, accompagnés de formulaires affichant les différentes structures d'appels. Elle est au format Access 2000.
V. Liens utiles▲
Arborescence dans un logiciel de gestion de stockArborescence dans un logiciel de gestion de stock proposé par f-leb et traitant de la récursivité dans Access.
Classification des données dans AccessClassification des données dans Access présentant deux exemples sur le même sujet.
Arrangements et combinaisons dans AccessArrangements et combinaisons dans Access décrivant des fonctions récursives permettant de générer des arrangements et des combinaisons.
VI. Remerciements▲
Je tiens à remercier Arkham46, lolo78 et dourouc05 pour m'avoir conseillé pour la réalisation de cet article, ainsi que Claude Leloup pour sa relecture.